What Are Multiple Representations?
Teaching Math With Representations
My 6th-grade math teacher used to say we had to learn math because, “You’re never going to carry a calculator in your pocket when you grow up!”
Well… now we all do. With smart devices at our fingertips, calculating an answer takes seconds.
So, if quick calculations are no longer the goal, what is the purpose of learning elementary math today?
It’s not just about answer-getting anymore. It’s about developing a deep understanding of numbers, noticing patterns, building number relationships, and being able to reason and communicate about mathematical ideas.
That’s where multiple representations come in.
If you’ve been hearing that phrase more often lately, there’s a reason. Today’s students aren’t just expected to follow one efficient path to an answer. They need to see math from multiple angles to make sense of it. But what are multiple representations in math? Why do they matter? And what does teaching with multiple representations in mind actually look like in the classroom?
In this post, I’ll answer all of that and share simple, effective ways to bring multiple representations into your upper elementary math lessons.
What Are Multiple Representations in Math and Why Do They Matter?
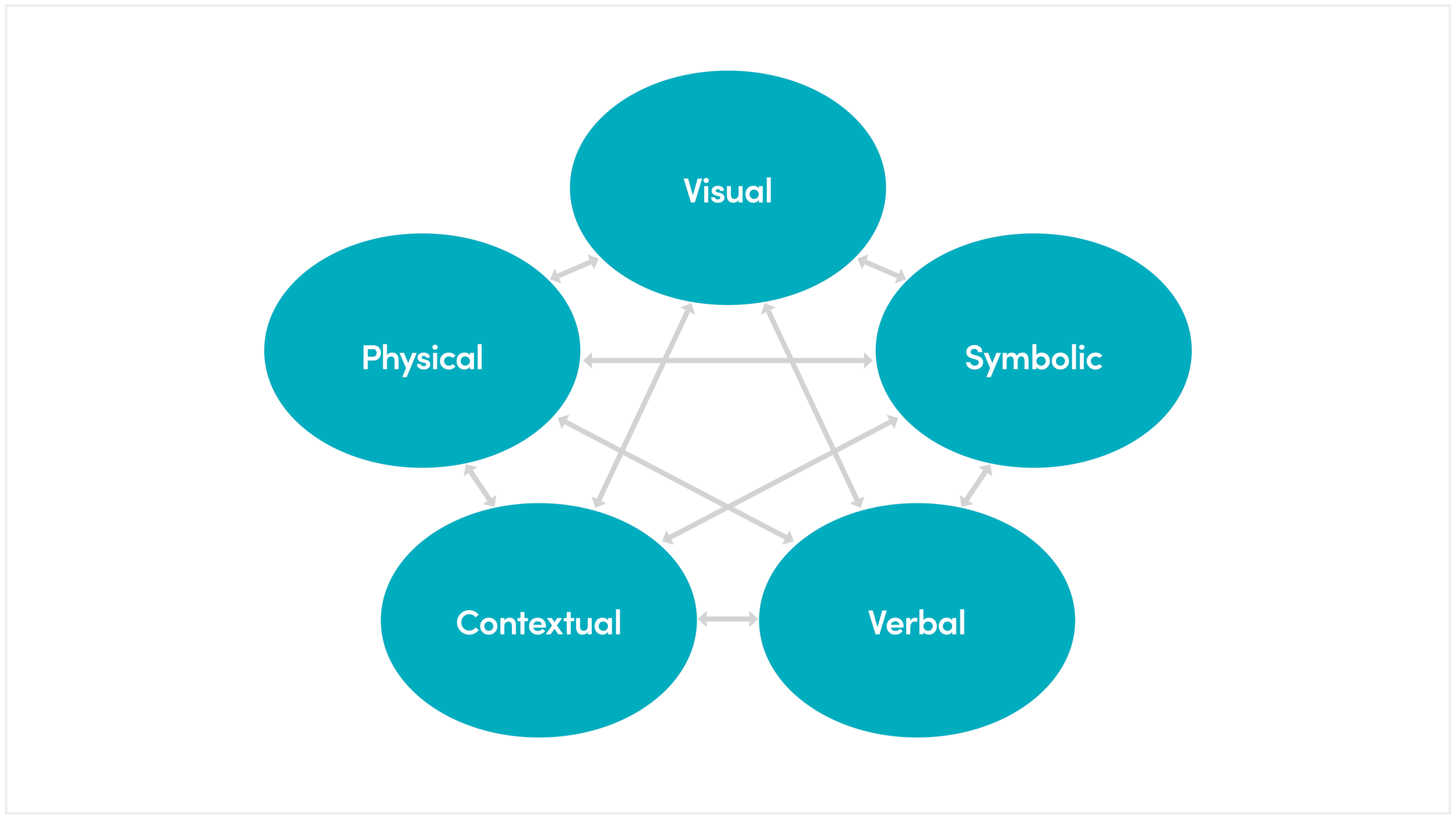
Over time, math educators have learned that students understand math more deeply when they can see it in different ways, such as with objects, drawings, words, and symbols. These different forms are called representations, and it’s how we show, explore, and communicate mathematical thinking. There are five key representations:
Physical: Using hands-on tools like base ten blocks, counters, fingers, folded paper, play money, or measurement tools
Visual: Drawing models such as number lines, graphs, arrays, area models, or tape diagrams
Symbolic: Using numbers and symbols in expressions, equations, or algorithms
Verbal: Talking or writing about math using both informal language and formal vocabulary
Contextual: Connecting math to real-world or imaginary situations that help give meaning to the numbers
So why do these different representations matter?
Research shows that when students engage with math through multiple representations, they develop a stronger, more flexible understanding. Each type of representation supports thinking in different ways: manipulatives help students see quantities, visuals help them organize their thinking, words help them explain their reasoning, and symbols help them generalize and solve problems efficiently.
But only using different representations isn’t enough. Research also shows that the real strength of multiple representations comes from helping students connect them. When students can move between representations, they build stronger mental models and have more reference points to draw from later. This not only boosts retention but also helps them catch errors, think critically, and apply their learning in new ways.
When students can move between a picture, a context, and a symbolic expression, they go beyond just following steps and instead show true understanding of how the math works. This idea is captured in the Lesh Translation Model, which shows how mathematical understanding grows as students connect and move between different representations.
The Lesh Translation Model
Let’s take a closer look at each of the five modes of representation and explore how a familiar upper elementary concept (multi-digit multiplication) can be represented in each one.
What the Five Modes of Representation Look Like
You may be thinking: I already know what each mode looks like. Physical representations use manipulatives, contextual ones connect to real life, visuals are drawings, and so on.
But here’s the thing: Truly understanding these modes means going deeper than just naming them. Most math concepts can be represented in several ways within each mode, and some of those representations are more abstract or sophisticated than others. For example, shading ⅔ of a rectangle and placing ⅔ on a number line are both visual representations, but the number line requires more advanced fraction reasoning and number sense.
To show how this works in action, let’s walk through how the problem 4 x 16 can be represented in each of the five modes.
Physical
When students are first introduced to multiplying larger numbers, they might start by modeling 4 groups of 16 using connecting cubes. From there, they might move to base ten blocks or arrange square tiles into an array.
While all of these are physical models, the array is more sophisticated because it organizes the thinking and sets the stage for strategies like breaking 16 into 10 and 6.
Visual
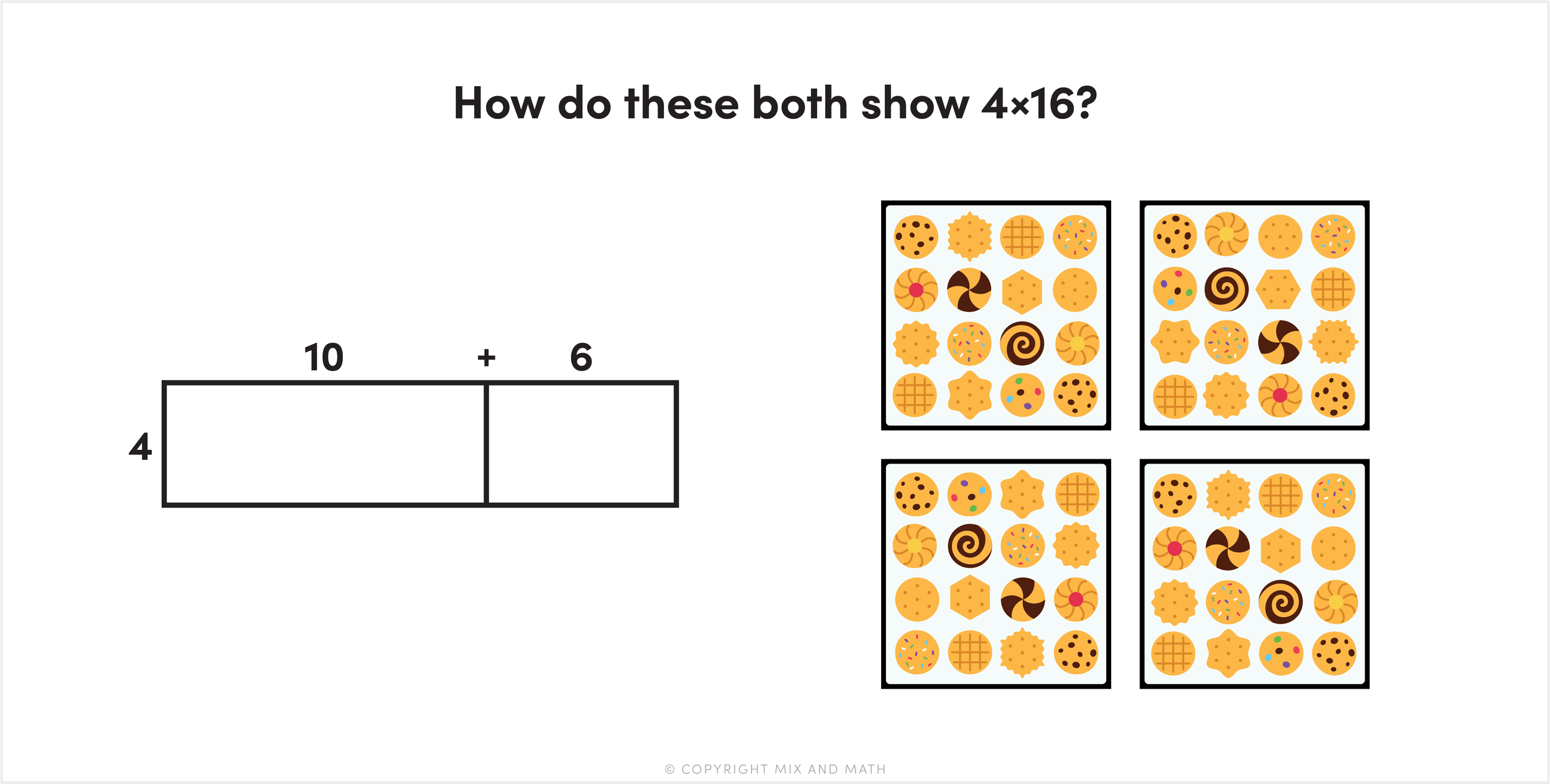
What students build with manipulatives can also be drawn. Using grid paper, they can sketch a 4 x 16 rectangle and shade it to show parts like 4 x 10 and 4 x 6. This is the foundation of the area model.
As students gain confidence, they often shift to more efficient drawings, such as the open area model, which shows the same structure without using a full grid. While individual units aren’t shown in the open model the way they are in the grid area model, students understand that each section still represents a certain number of square units.
Symbolic
As students decompose numbers using area models, they should also write expressions to match. In this case, 4 x 16 becomes (4 x 10) + (4 x 6) — exactly what we see in the partial products algorithm!
Over time, students can connect this thinking to a standard algorithm, which is simply a more efficient way of recording the same idea.
Contextual
As students work with other representations, we want them to stay grounded in real-world meaning. That may look like a teacher saying, “You have 4 boxes with 16 cookies each.”
But it’s also important to let students generate their own contexts. For example, show them an array and ask, “What real-life situation could this represent?”
Verbal
As students use each type of representation, talking about the math helps solidify their understanding. You might hear, “There are 4 boxes with 16 cookies each, so that’s 4 groups of 16.” Or, “4 times 16 is the same as 4 groups of 10 and 4 groups of 6.”
When students can explain their thinking clearly and accurately, it’s a strong sign they understand the math, not just the answer.
When students can represent a single idea with all five modes, they begin to see that math isn’t just about steps; it’s about understanding relationships and structure. Each mode offers a unique lens, and when students connect those lenses, their understanding gets deeper and more durable.
How to Teach With Multiple Representations
OK, so how do we actually incorporate multiple representations into our math lessons? Great question! No matter the topic, these six strategies can help make teaching with multiple representations both manageable and meaningful.
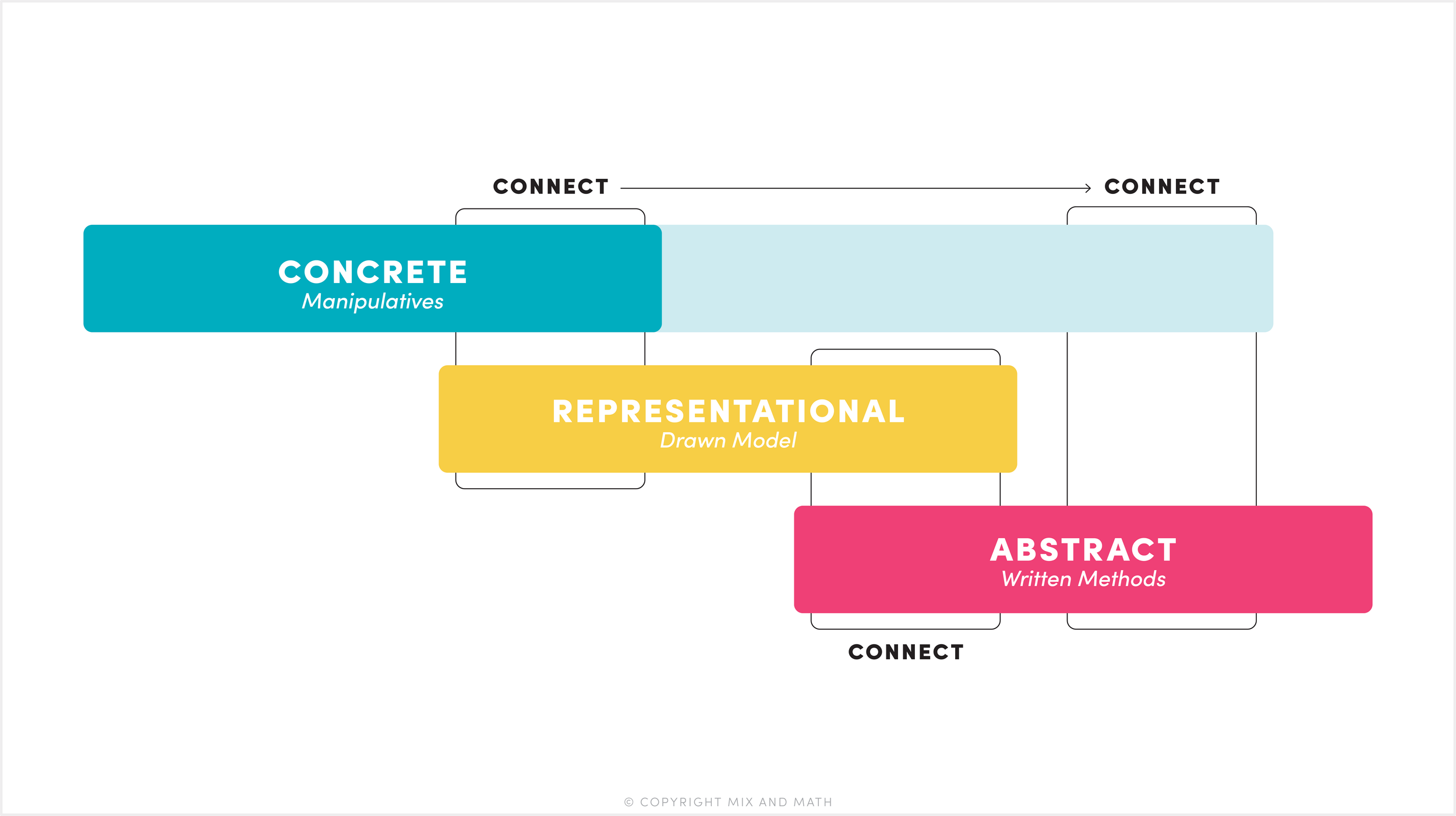
Tip 1: Follow the CRA Sequence
One of the most well-known ways to structure multiple representations is through the CRA sequence: Concrete (Physical), Representational (Visual), and Abstract (Symbolic). Research has shown again and again that following the CRA sequence benefits all learners in learning math conceptually.
Want to learn more about CRA? Check out A Guide to the CRA Model!
The goal isn’t to follow the sequence rigidly or check off stages one by one. It’s to help students build connections between the stages. And while CRA focuses on physical, visual, and symbolic representations, it’s important to ground them in verbal and contextual representations to support deeper meaning-making.
What it could look like:
A student builds 3 x 12 using cubes (concrete), draws an array of 3 rows of 12 (representational), and then writes (3 x 10) + (3 x 2) to match what they made (abstract).
Later, they might solve 3 x 12 using the standard algorithm, and a class discussion helps connect the steps back to the earlier models.
Tip 2: Explicitly Teach Representations
While some representations come naturally to students, others must be modeled and taught intentionally. Don’t be afraid to introduce new representations or guide students in how to use and connect them.
Try this:
During small group instruction, if a student uses manipulatives to solve a problem, model how to show the same idea with a drawing or equation. Say something like, “Here’s another way to show what you just did.”
After students solve a problem in different ways, highlight a few models during the class share-out and lead a discussion on how each connects.
Use matching or sorting activities in which students pair a story problem, equation, visual model, and hands-on tool that all represent the same idea.
Tip 3: Connect Representations Across Modes
It’s not enough to simply expose students to different representations! We also need to help students make meaningful connections across them.
Try this:
Use math mats or graphic organizers that prompt students to show their thinking in at least two different ways.
Partner up students to problem-solve: one uses manipulatives while the other draws or writes equations. Then they explain their models to each other and discuss how they show the same thinking in different ways.
If a student solves a problem with a symbolic algorithm, ask them to model the same steps using base ten blocks or a drawing to show the meaning behind the procedure.
Tip 4: Connect Representations Within a Single Mode
Just as we can connect ideas across modes, it’s also important to help students see relationships within a single mode. Many concepts can be shown in multiple ways within the same type of representation. Some of those representations are more concrete, while others are more abstract or efficient.
Think back to our examples of 4x16: both a grid area model and an open area model are visual, but the open area model is more abstract and efficient because it doesn’t show every unit. Similarly, the partial products strategy and a standard algorithm are both symbolic, but a standard algorithm is more condensed.
Helping students move from less to more sophisticated representations within the same mode supports a smooth shift toward more efficient models while still keeping their thinking grounded in understanding.
Try this:
Have students match different visual models (or different symbolic or contextual representations) that show the same math idea.
After one student shares their thinking out loud, ask another to restate it in their own words or offer a new explanation.
After solving a word problem, challenge students to write a different real-world situation that could match the same equation or model.
Tip 5: Include Multiple Representations in Assessments
If we value multiple representations during instruction, we must reflect that in how we assess student understanding. If our assessments only ask students to solve problems using numbers and symbols, we’re missing a key piece of the picture.
Try this on assessments:
Ask students to solve a problem, show their thinking with a model, and write a matching story problem.
Provide two different models of the same situation and ask students to explain how they represent the same math.
Use exit tickets to check which representations students are confident using, and use that data to inform your instruction.
Tip 6: Teach Students to Choose Representations Strategically
One of the ultimate goals of using multiple representations is to help students develop a toolbox of strategies they can use flexibly. But just having the tools isn’t enough — students also need to know which tool to use and why.
Try this:
Give students several problems and have them match each to the most helpful representation. Then, ask them to explain why that representation was useful for that situation.
Encourage reflection with prompts like: “Was the model you used helpful?” or “Would another way have worked better?”
During discussions, ask students to justify their choice of representation and explain it to others.
Wrapping it Up
At its core, teaching with multiple representations isn’t about adding more to your plate. It’s about helping students truly understand math, not just follow steps to get the right answer. When students can see math in different ways, they build stronger number sense, more flexible thinking, and deeper conceptual understanding. They start to see the connections between models, equations, and real-life situations. And most importantly, they grow into confident, capable mathematical thinkers.
If this feels a little overwhelming, that’s okay. You don’t have to change everything at once. Start small by being more intentional about naming and connecting representations during your regular instruction. Try one of these simple strategies this week:
Model two different ways to represent the same problem.
Ask students how a drawing connects to an equation.
Choose one task where students show their thinking in more than one way.
Over time, these small shifts add up. And, as your students become more comfortable with multiple representations, you’ll not only see deeper understanding; you’ll also see more joy, confidence, and engagement in your math classroom!