What is the CRA Model in Math?
I recently had lunch with my mentee, a second-year teacher who somehow manages to wrangle a classroom full of first graders (in heels!) without breaking a sweat. Between bites of tacos, she shared something I hear from teachers all the time:
“My students seem to get it during the lesson, but they seem totally lost when they’re asked to use the same concept in a slightly different way.”
My go-to response? Teach through the Concrete–Representational–Abstract (CRA) model. It’s one of the most effective ways I’ve found to help students build deep understanding and see how math ideas fit together.
My mentee remembered hearing about CRA in her credential program but admitted she never really understood what it meant or how to use it in real classrooms. If you’ve ever felt the same way, this post is for you!
What Is the CRA Model?
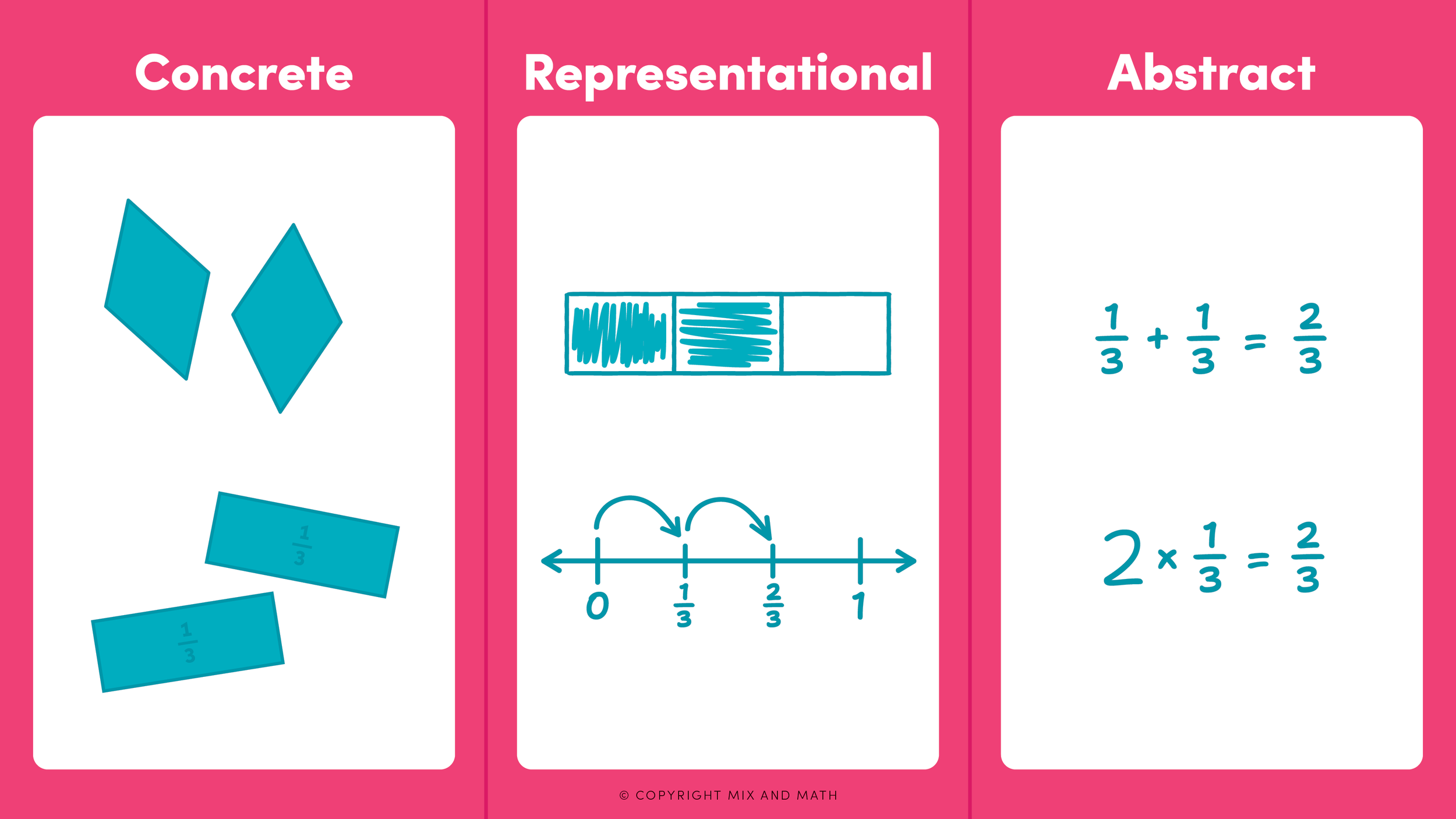
Also called Concrete-Pictorial-Abstract (CPA) or Concrete-Semi Concrete-Abstract (CSA), the CRA model is a research-based approach to teaching math that helps students move from hands-on exploration to abstract thinking through three stages:
Concrete – Using physical tools and manipulatives
Representational (Pictorial/Semi Concrete) – Drawing pictures or diagrams
Abstract – Using numbers, symbols, and equations
Moving through the three phases as students learn math is not just helpful, it’s also incredibly powerful. Research shows that students who learn through the CRA model:
Develop a deep, flexible understanding of math concepts.
CRA supports concept development, not just memorization. By starting with hands-on materials, students build a mental model that helps them visualize concepts, even when the manipulatives are no longer available.
Stay engaged and confident.
Studies show that manipulatives and visual models help reduce math anxiety and improve students’ belief in themselves as mathematicians. When students see the math, it feels less abstract and more doable.
Build stronger number sense and mental math skills.
CRA emphasizes relationships between numbers and operations, which lays a strong foundation for mental strategies and estimation.
Transfer learning to new and real-world situations.
When students understand why a strategy works, they can apply it in new contexts.
In short, CRA helps students become thinkers and problem-solvers, not just answer-getters.
A Closer Look at Each CRA Phase
Concrete
In this phase, students use physical objects to act out and model math. This might include:
Traditional manipulatives: base-10 blocks, pattern blocks, fraction tiles, play money, counters, cubes, etc.
Everyday objects: beans, sticky notes, paper, measuring cups, food — anything that helps model the math
This stage is all about experiencing the math, not memorizing steps. Students explore concepts by physically working through them, using tools to try out strategies and make sense of what’s happening.
The goal of the concrete phase is to build meaning behind the math.
Because it's hands-on, the concrete phase gives students space to explore and make sense of math before they jump into written methods. They're focused on what's happening, not just finding an answer.
The more students physically act out math processes, the stronger their connections will be later when they move to drawings or symbolic equations. These experiences help students recognize math in real-life situations and understand operations more deeply.
While the concrete phase often comes first, it shouldn’t be a one-and-done. Students can (and should!) return to manipulatives even after learning written procedures. In fact, revisiting concrete tools after teaching an algorithm is one of the best ways to make sure students understand the math, not just follow steps.
Representational/Pictorial/Semi-Concrete
In the representational phase, students move from hands-on models to drawn models. They use pictures and diagrams to represent what they did with manipulatives during the concrete stage.
Some common visual representations include:
Drawn fraction models
Number lines
Pictures of base-ten blocks or fraction tiles
Area models
Arrays
Tape diagrams
Dots, stars, or circles
Tally marks
This phase is about putting math into a written form. Students often begin by drawing exactly what they used, such as sketching out the pattern blocks or counters they manipulated. Over time, their drawings become more symbolic and less tied to specific tools.
The representational stage serves as a bridge between doing the math concretely and doing it abstractly.
To support deep understanding, it's important to blend this phase with both the concrete and abstract stages. That means you may go back and forth between drawing and using manipulatives or between drawing and writing equations to help students see how all the representations connect. More on this a bit later!
Abstract
In the abstract phase, students move to symbolic representations, using numbers and symbols instead of manipulatives or drawings. This is often the most efficient stage for solving problems.
The purpose of the abstract phase is to represent math efficiently but not at the expense of understanding.
Students can’t deeply understand an abstract method if they jump straight to it. The power of CRA is in the thinking developed during the concrete and representational phases. When students have that foundation, the abstract phase starts to make sense on its own. Students are not just memorizing steps. Instead, they’re seeing the why behind them.
Tips for Teaching Using the CRA Model
So, while the abstract phase is where we often end up, it's not where understanding begins. The learning happens through the connections students make between all three phases. This is the real magic behind CRA.
Here are a few key tips to keep in mind as you bring CRA to life in your classroom:
The Stages Are Not Isolated
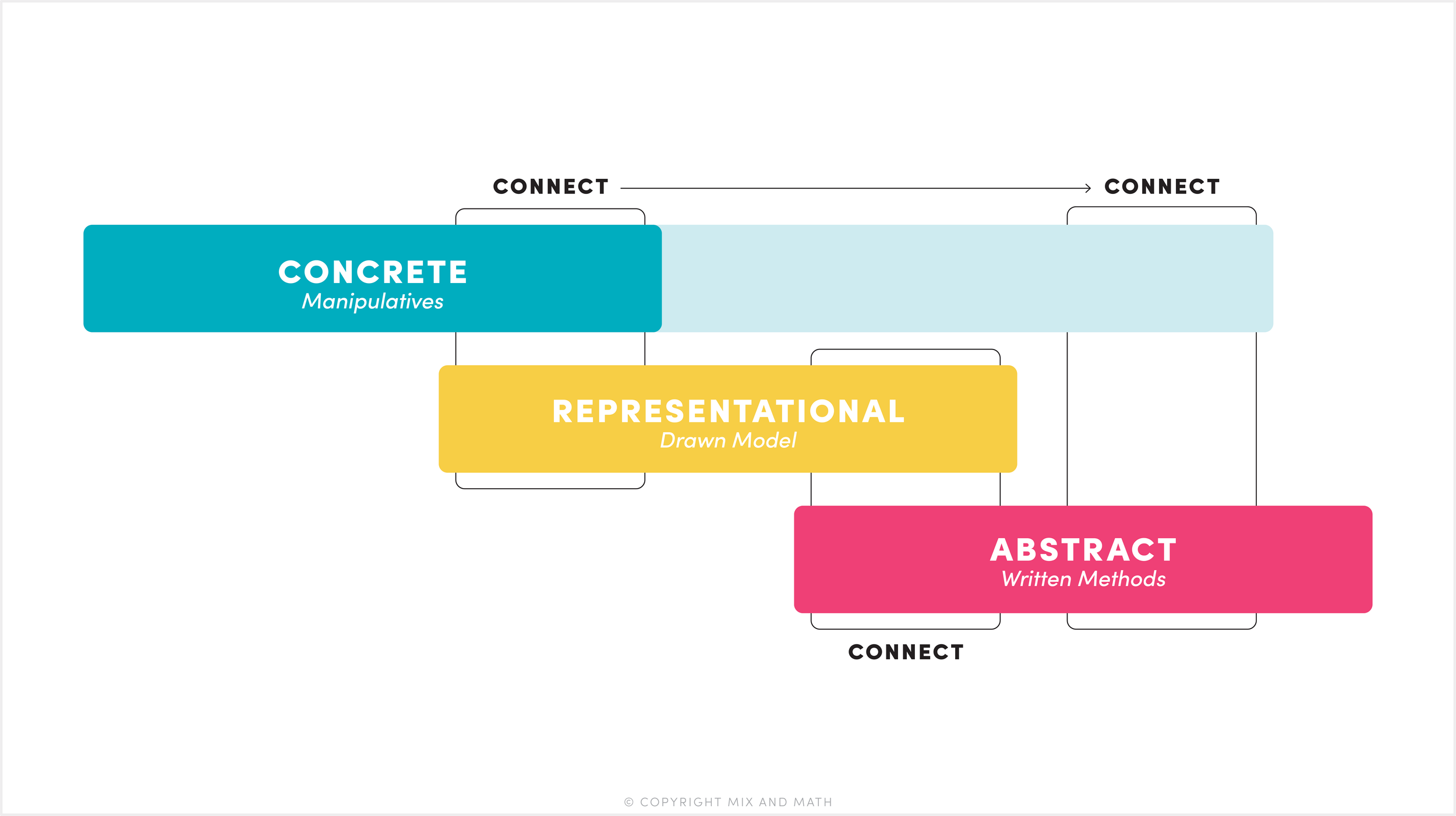
Think of the phases as a gradual progression, not separate buckets. Students shouldn’t feel like they’re learning three different strategies (this can actually overwhelm them)! Instead, they should see it as one concept represented in different ways.
Yes, there are times when students will work entirely within one phase, and that’s valuable. But the most effective learning happens when they bridge two or more stages. Once a student starts working in the representational phase, they should still connect their representations back to concrete manipulatives. Likewise, a student working in the abstract phase should connect their symbolic representations to drawn diagrams and concrete manipulatives.
Here’s what that might look like:
Students use manipulatives and sketch what they built, then write an expression that represents it.
Students solve a problem with an algorithm or symbolic method and then show what they did in the procedure with a drawn or concrete model.
Avoid Over-Reliance on One Stage
Each stage in the CRA model serves an important purpose, but the goal isn’t to keep students in one phase forever. We want to gradually move them toward more abstract thinking, where they can solve problems efficiently and explain their reasoning.
Some critics argue that students won’t always have access to manipulatives in real-world situations, and that’s true. But manipulatives aren’t the end goal — they’re a starting point. The concrete and representational stages help students build strong mental models they can lean on when working symbolically.
As students grow in understanding, it’s important to slowly fade out one model while helping them bridge to the next. Here are a few ways to support that shift:
Choose numbers strategically.
Some numbers (like 15, 1½, or 0.3) are easy to model with concrete tools like blocks or counters. Others (like 67 or 4.89) are more difficult to model with manipulatives, but they are easily modeled with pictures or symbols. When introducing a concept, stick with easy-to-model numbers. As students progress, mix in more challenging numbers to move them toward more efficient representations.Look for windows into student thinking.
Use warm-ups, exit tickets, and small groups to see how students are reasoning. Are they using manipulatives? Drawings? Equations? This gives you insight into what they understand and helps you decide how to guide them forward.Intentionally fade models as understanding grows.
Start by asking students to solve with manipulatives and represent their work with drawings and equations. Once they’ve shown understanding, have those who are ready solve using only a visual model or just numbers.
In short, students shouldn’t get stuck in one stage or skip ahead too quickly. The effectiveness of CRA comes from moving flexibly between stages and building lasting understanding along the way.
Keep Manipulatives in the Mix
Manipulatives aren’t just for beginners! They’re useful, powerful, and important tools that hold an idea so we can think more deeply about it. They’re front and center in the concrete phase, but they also help carry conceptual understanding into representational and abstract thinking.
This means:
Don’t pack away the tools as soon as students start drawing or writing equations.
Don’t assume that older students “don’t need” manipulatives. They often need them more when concepts get more complex. As students are pushed to new levels of thinking, they frequently need to spiral back to concrete and pictorial representations.
Take fractions, for example:
When students learn to add and subtract fractions, manipulatives help them visualize what this looks like. Students connect these to drawn fraction models, number lines, and eventually, an algorithm.
Later, when students learn about multiplying fractions, return to those same manipulative models to help ground students’ understanding in previous learning.
By continuing to return to manipulatives and reinforcing the connections between physical models, drawings, and equations, you help students build lasting, flexible understanding. That’s the heart of CRA, and it’s what turns students into conceptual math thinkers.
The Bottom Line: What You Need to Know About CRA
Concrete = math manipulatives and other physical tools
Representational = drawn models
Abstract = symbols and algorithms
Remember, the phases are NOT isolated… blend them together!
Now that you understand the basics of the CRA model, dive more deeply into using multiple representations in math in our FREE Make Math Hands-On workshop! In this 90-minute workshop, you’ll learn:
The #1 mistake we all make with manipulatives (and how to fix it)
How to use them in a way that actually deepens understanding
A framework for using manipulatives with any concept in your curriculum
If that sounds helpful, I’d love to have you join us! It's completely FREE, and you'll walk away with ideas you can use immediately. You'll also receive 24 FREE math manipulative task cards and a certificate of completion for 1.5 hours! Click below to save your spot in an upcoming workshop!