If you’ve ever taught multiplicative comparisons, you’ve probably seen the blank stares, noticed confused looks, or heard a student ask, “So we add, right?” Even adults pause when they hear a question like, “Zoe has 4 times as many marbles as Raj. If Zoe has 40 marbles, how many marbles does Raj have?”

Why are these questions so tricky?

It’s because our brains were taught to think additively. We’re used to asking, “How many more?” or “What’s the total?” However, in upper elementary grades, students are introduced to a whole new way of thinking: multiplicative reasoning. It’s a shift in how students see and work with numbers.

If you want to take the confusion out of multiplicative comparisons for your students, here are three tips to help you do just that!

Make the Difference Between Additive and Multiplicative Comparisons Clear

In early elementary, students learn to answer questions like:

“Seth has $4 and Omar has $12. How many more dollars does Omar have than Seth?”

This is an additive compare problem, or additive comparison. Students solve this by thinking: “How much more is 12 than 8?” They could use addition (4 + ___ = 12) or subtraction (12 - 4 = ___) to find the answer of $8.

Now, here’s the twist:

“Seth has $4 and Omar has $12. How many times as many dollars does Omar have as Seth?”

This is a multiplicative compare problem, or multiplicative comparison. Students solve this by thinking: “How many times as much as 4 is 12?” They could use multiplication (4 x ___ = 12) or division (12 ÷ 4 = ___) to find the answer of 3.

This is an entirely different way of relating numbers. The units students compare are now groups of 4, not individual dollars. Seeing a group of 4 as one unit (the mathematical term for this is “unitizing”) instead of 4 individual dollars is a major conceptual leap!

Simply put, the difference between these comparisons is that additive comparisons ask, “How much more?” whereas multiplicative comparisons ask, “How many times as much?”

Unfortunately, students don’t always recognize this difference, even though these are two very different questions.

Here’s what can be frustrating when teaching multiplicative comparisons: students often fall back to relying on additive thinking, especially if they haven’t had enough experience seeing how the two comparison types differ. The language can be very tricky, and students must be taught explicitly to notice these differences.

To make this distinction clear:

Give students two problems with the same context but different types of comparisons, as we saw above.
Then, ask students what they notice about the similarities and differences between these two problems.

These side-by-side comparisons can lead to meaningful discussions and give students a deeper understanding of the difference between additive and multiplicative comparisons.

Expose Students to All Three Multiplicative Comparison Situations

Up to this point, students have worked with multiplication and division problems with equal groups and arrays. Now, we want to help students understand a new-to-them type of multiplication and division problem: compare problems.

What makes multiplicative comparisons extra tricky? There isn’t just one kind! There are three different types of comparison situations, and they all use similar language. The difference lies in what’s unknown.

Let’s walk through all three…

Situation #1: Larger Unknown

Larger unknown is the multiplicative comparison situation that is typically the easiest for students to understand. In larger unknown situations, we know the smaller quantity and how many times greater the larger quantity is, but we don’t know the larger quantity.

In our example, we know the blue beads must be a larger quantity than the red beads because it says the number of blue beads is 3 times as much as the number of red beads. Since we know Sofia has 5 red beads, we can multiply 3 x 5 to find the number of blue beads, 15.

Situation #2: Smaller Unknown

With smaller unknown situations, multiplicative comparisons can get especially tricky. To solve these comparisons, we must focus on what we know. We know the larger quantity and how many times greater it is than the smaller quantity, but we do not know that smaller quantity.

In the example, we know Sofia has 15 blue beads and that this is 3 times as many as the number of red beads. To find how many red beads she has, we can think: “15 is 3 times as much as what number?” A division equation (15 ÷ 3) or a missing-factor multiplication equation (15 = 3 × ?) shows that Sofia has 5 red beads.

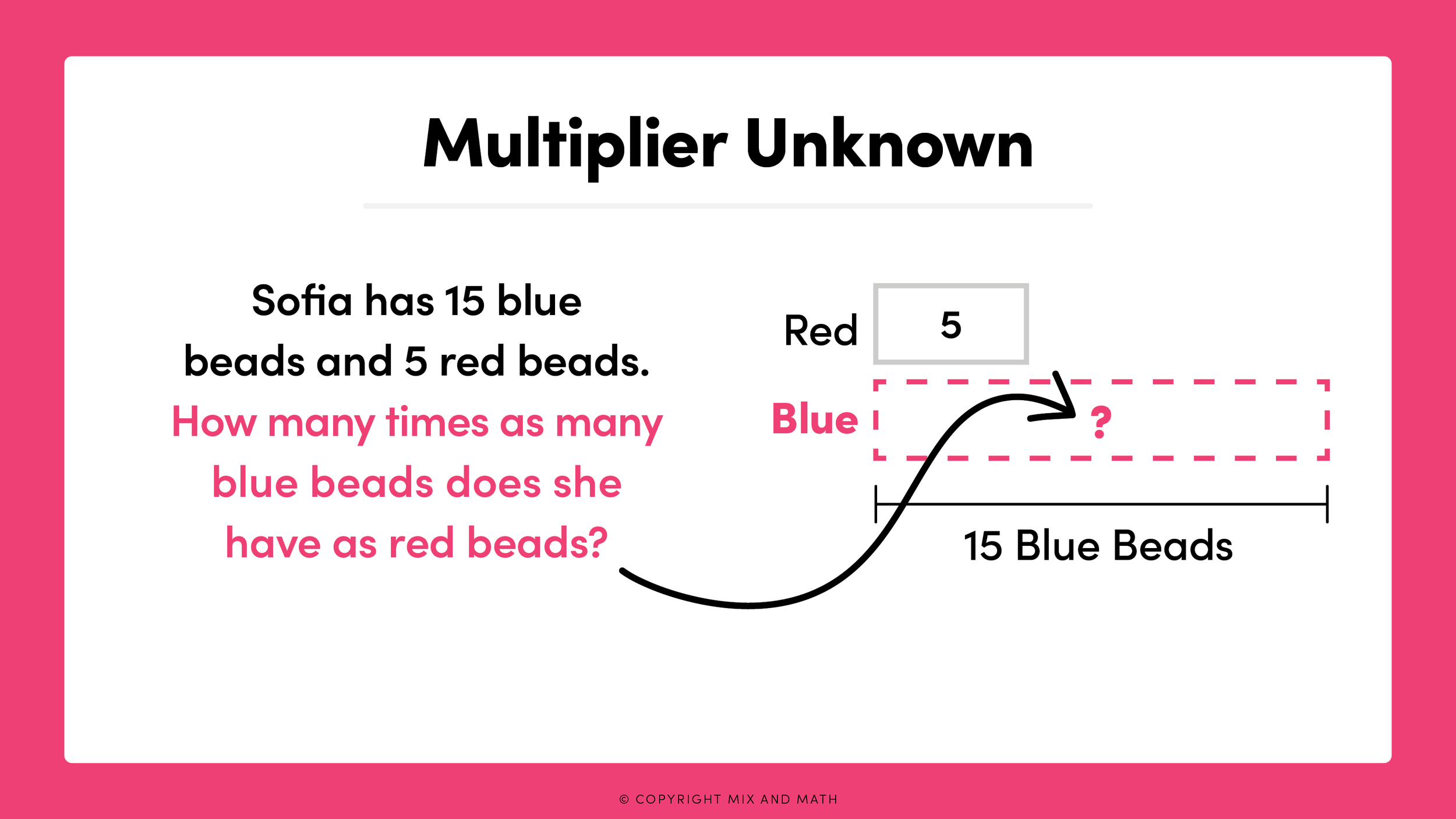
Situation #3: Multiplier Unknown

Multiplier unknown situations are another kind of multiplicative comparison that can have especially tricky language for students. Again, it’s important to focus on what we know to solve these problems. In multiplier unknown problems, we know the smaller and larger quantities, but we need to determine how many times greater the larger quantity is than the smaller one.

In the example, we know the larger quantity is 15 blue beads, and the smaller quantity is 5 red beads. To figure out how many times as much 15 is as 5, we can use multiplication with a missing factor (15 = ? × 5) or division (15 ÷ 5 = ?). Either way, we find that the multiplier is 3.

Students often assume “times” means multiply, but as we see from these situations, we can’t just multiply the numbers we see to solve these multiplicative comparison problems.

The structure of the problem and the unknown information determine how we approach solving it. Be sure to expose students to all three types so they get to practice identifying what they know, what they’re trying to find out, and what strategy they could use to solve.

Connect Multiplicative Comparisons to the Real World

Multiplicative comparisons aren’t just a one-time concept. They show up everywhere in math:

Place Value Relationships: 30 is worth 10 times as much as 3.
Measurement Conversions: 1 foot = 12 inches, so the number of inches is always 12 times as many as the number of feet.
Fractions and Ratios: Equivalent fractions are just comparisons! It takes 2 eighths to make 1 fourth, so the number of eighths will always be 2 times as many as the number of fourths.

Let’s look at a real-world measurement example…

My tomato plant is 3 feet tall. How many inches tall is my tomato plant?

We know that the tomato plant is 3 feet tall, and we also know that 1 foot is equivalent to 12 inches. This means we will need 12 times as many inches as feet to measure the plant’s height. 3 x 12 = 36 inches, so the plant is 36 inches tall.

Real-world examples help students see what “times as much” really means. When we show students that multiplicative comparison language and reasoning shows up in measurement, place value, and even fractions, it gives them the opportunity to practice it in other contexts.

When students make connections across different math concepts they start to make sense of math at a deeper level, which leads to a deeper understanding. Ultimately, we want students to be able to apply multiplicative reasoning across any math concept. When students see these real-world examples, they can make connections between these different math concepts, leading to a deeper understanding that lasts.

Multiplicative comparisons can be tricky at first, but when you intentionally expose students to all three comparison situations and make real-world connections, they don’t have to be confusing. As a teacher, when you:

Make the difference between additive and multiplicative comparisons clear
Teach all three multiplicative comparison situations
Ground the work in real, relevant examples

You are setting your students up for success with multiplicative comparisons and many future math concepts. So let’s focus on moving beyond just solving for an answer and help our students truly make sense of multiplicative thinking!

3 Tips For Teaching Multiplicative Comparisons So They Stick!

Make the Difference Between Additive and Multiplicative Comparisons Clear